Mechanika tuhého tělesa

Tuhé těleso

• ideální těleso
  • skupina hmotných bodů, jejichž vzájemná vzdálenost se nemění
  • ve skutečnosti neexistuje
• nemění tvar ani objem působením libovolných sil
• ve skutečnosti neexistuje
• použití v případech
  • kdy lze deformační účinky sil zanedbat
  • nelze těleso nahradit hmotným bodem

Síly

• působiště síly lze v tělese libovolně posouvat po vektorové přímce síly
• sčítání sil
  • síly se stejným působištěm
    • rovnoběžné se jednoduše sečtou
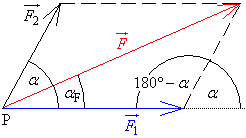
    • u různoběžných se doplní rovnoběžník a výslednicí je úhlopříčka
      • { height=150 }
      • pro výpočet použijeme součet dvou vektorů, v případě kolmých sil můžeme i goniometrické funkce
  • síly s odlišným působištěm
    • různoběžné
      • síly posuneme na stejné působiště
    • rovnoběžné
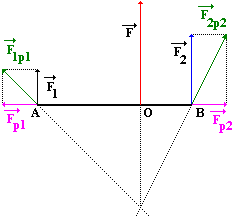
      • síly si musíme "zrůznoběžnit" a pak sečteme jako dvě různoběžné se různým působištěm, výslednici nakonec přesuneme do roviny s původními silami
      • { height=150 }
      • výpočtem lze působiště síly najít nepřímou úměrou $\frac{|AO|}{|OB|} = \frac{F_2}{F_1}$
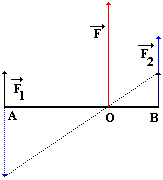
      • lze také použít trik - jednu ze sil otočíme do protisměru (vynásobíme vektor $-1$), spojíme konce sil přímkou a tam kde tato přímka protíná přímku mezi působišti obou sil, tam působí výsledná síla
      • { height=150 }
  • dají se stejně tak rozkládat, jen opačně než sčítání
  • nelze sčítat síly mimoběžné
• těžistě tělesa
  • působiště tíhové síly působící na těleso v homogenním tíhovém poli
  • v pravidelných tělesech (koule, krychle) tvořených homogenní hmotou se nachází v geometrickém středu tělesa
  • můžeme ho zjistit zavěšením tělesa
    • nachází se v průsečíku všech těžnic - přímek vedoucích z bodu zavěšení kolmo dolů skrz těžiště

Poloha tělesa

• lze definovat pomocí 3 bodů na nebo v tělese, které neleží v přímce
  • v případě 3 rozměrného prostoru 9 různých souřadnic, z nichž je potřeba pouze 6 (zbylé se dají dopočítat pomocí trojúhelníků)
• rovnovážná poloha nastane, když součet všech sil působících na těleso je nulový zároveň s výsledným momentem sil (viz dále)
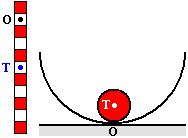
  • stálá (stabilní) rovnovážná poloha je takové poloha, do které se těleso po vychýlení vrácí
    • například kulička v důlku
    • { height=60 }
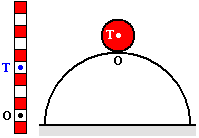
  • vratká (labilní) rovnovážná poloha je taková poloha, do které se těleso po vychýlení nevrací
    • například kulička na kopečku či tyč stojící na špičce
    • { height=60 }
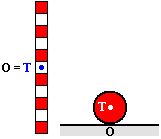
  • volná (indiferentní) rovnovážná poloha je taková poloha, u které se vychýlením nezmění výsledná síla ani moment a těleso zůstává v konstantní vzdálenosti od původní polohy
    • například koule na vodorovném podkladu
    • { height=60 }

Pohyb tělesa

• lze rozdělit na 2 typy, výsledný pohyb vzniká složením obou
• posuvný pohyb (translace)
  • všechny body tělesa konají pohyb po stejných, jen vůči sobě posunutých trajektoriích
  • rychlost všech bodů tělesa je stejná
  • lze převést na pohyb hmotného bodu (nejčastěji těžiště)
  • kinetická energie tělesa je $E = \frac{1}{2}mv^2$
    • stejné jako u hmotného bodu
    • energie, kterou je potřeba vynaložit na uvedení tělesa do pohybu z klidového stavu
• otáčivý pohyb (rotace)
  • všechny body tělesa konají pohyb po kruhových trajektoriích, jejichž středem je osa rotace
  • rychlost otáčení definujeme jako úhlovou rychlost $\omega$
    • $\omega = \frac{\Delta\varphi}{t} = \frac{v}{r}$
      • změna úhlu (v radiánech) za čas
      • rychlost otáčejícího se bodu tělesa lomená vzdáleností od osy otáčení
    • je vůči jedné ose otáčení u všech bodů stejná
  • energie rotujícího tělesa je dána součtem kinetických energií všech bodů
    • lze vypočítat z úhlové rychlosti a momentu setrvačnosti (viz moment setrvačnosti)
  • k posouzení účinku síly na otáčivý pohyb se používá moment síly
  • k posouzení energie potřebné na roztočení tělesa se používá moment setrvačnosti

Moment síly

• používá se k posouzení otáčivých účinků síly na těleso
• vektorová fyzikální veličina
• symbol $M$
• odvozená jednotka newton metr $Nm$
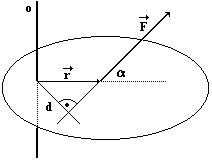
• výpočet
  • $\vec{M} = \vec{r} \times \vec{F}$
    • $\vec{r}$ je vektor kolmý na osu otáčení, vede z ní až do působiště síly
      • směr vektoru lze určit podle pravidla pravé ruky
    • $\vec{F}$ je vektor síly působící na tuhé těleso
    • {height=100}
  • $|\vec{M}| = d \cdot |\vec{F}| = |\vec{F}| \cdot |\vec{r}| \cdot \sin{\alpha}$
    • $d$ je kolmá vzdálenost od osy otáčení k vektoru síly (viz obrázek výše)
    • $\alpha$ je úhel mezi vektorem $\vec{r}$ a $\vec{F}$
  • momentová věta
    • $\vec{M_c} = \sum_{i=0}^{n} \vec{M_i}$
    • momenty jednotlivých sil vektorově sčítáme, abychom zjistili celkové rotační účinky na těleso
    • pokud je výsledný moment nulový, rotační účinky nejsou žádné
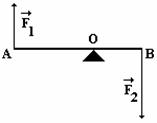
      • příkladem využítí je dvouzvratná páka
      • {height=80}
  • dvojice sil
    • současné působení dvou rovnoběžných sil stejně velkých opačného směru působících v různých místech (na různých vektorových přímkách) tuhého tělesa
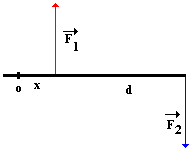    • { height=100 }
    • translační účinky obou sil se vyruší, takže těleso se nikam nepohybuje
    • rotační účinky ale nemůžeme zanedbat
      • u obou sil proto musíme spočítat jejich moment
      • pomocí momentové věty určíme celkové rotační účinky na těleso
    • rameno dvojice sil je vzdálenost mezi silami ($d$)
    • velikost výsledného momentu je $D = F\cdot d$, kde $F = F_1 = F_2$

Moment setrvačnosti

• vyjadřuje míru setrvačnosti při rotačním pohybu
• závisí na rozložení hmoty v tělese a na umístění osy otáčení
  • $J = \sum_{i=0}^{n} m_i r_i^2$
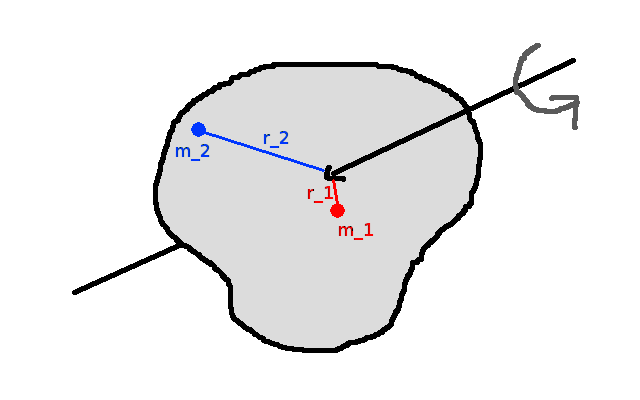  • { height=150 }
  • každý hmotný bod tělesa má vliv na moment setrvačnosti
    • čím dále je bod dále od osy otáčení, tím více přispívá k momentu setrvačnosti
    • roztočit dlouhý válec je náročnější než kouli o stejné hmotnosti
• symbol $J$, někdy také $I$
• odvozená jednotka ${kg}\cdot{m}^2$
• využití
  • kinetická energie rotace
    • $E_k = \frac{1}{2} J {\omega}^2$
    • energie potřebná k roztočení tělesa z klidového stavu na určitou úhlovou rychlost ($\omega$)

\pagebreak

Příklady

Moment síly

Zadání

Ve vrcholech obdélníkové desky (rovnoběžník $ABCD$) se stranami $a = 30\ cm$, $b = 40\ cm$ působí síly $F_1 = 10\ N$, $F_2 = 20\ N$, $F_3 = 30\ N$, $F_4 = 40\ N$. Deska je otáčivá kolem osy, která je kolmá na desku a prochází vrcholem $A$. Jaký je výsledný moment sil působících na plotnu?

\

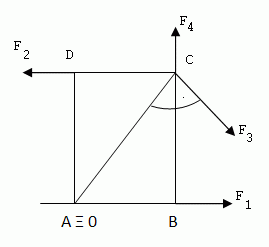Řešení

\

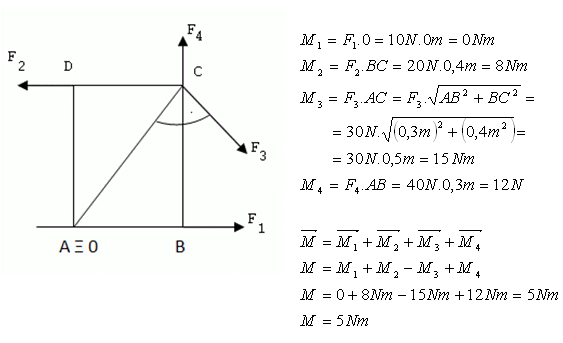Výsledný moment sil je $5\ Nm$.

Skládání sil

Zadání

Tyč má délku $1,2\ m$. Na její koncích jsou zavěšeny závaží s hmotnostmi $5\ kg$ a $7\ kg$. Kde je třeba tyč podepřít, aby zůstala v rovnováze?

\

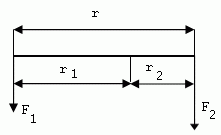Řešení

Na řešení použijeme momentovou větu. Protože na tyč nemají působit žádné rotační účinky, musí být celkový moment nulový.

$r = 1,2\ m$, $m_1 = 5\ kg$, $m_2 = 7\ kg$, $F_1= 50\ N$, $F_2 = 70\ N$

$\begin{aligned} r_1+r_2 &= r \\ F_1r_1 - F_2r_2 &= 0 \\ F_1r_1 &= F_2r_2 \\ \end{aligned}$ $\begin{aligned} r_1+r_2&=1,2 \\ r_2&=1,2-r_1 \\ \end{aligned}$ $\begin{aligned} 50\cdot r_1 &= 70 \cdot r_2 \\ 50\cdot r_1 &= 70\cdot\left(1,2-r_1\right) \\ 50\cdot r_1 &= 84-70\cdot r_1 \\ 120\cdot r_1 &= 84 \\ \end{aligned}$

$\underline{r_1=0,7\ m,\ r_2=0,5\ m}$

Tyč je třeba podepřít ve vzdálenosti $0,7$ metru od síly $F_1$.