Elektrické pole

Elektrický náboj

• $Q=\left[C\right]$
• Coloumb je odvozená jednotka SI
  • Náboj jednoho Coloumbu porojde průřezem vodiče při proudu jednoho ampéru za $1\ s$.
  • $C=A \cdot s^{-1}$
• Poprvé pozorován ve starověku u jántaru (elektron)
  • Projevuje se praskáním a drobným jiskřením
• vyjadřuje velikost schopnosti působádit elektrickou silou
  • Pro představu
    • Elektrický náboj vyjadřuje vlastnost, která je spojena s určitými interakcemi (elektrické pole) mezi tělesy podobně jako je hmotnost spojená s interakcemi v gravitačním poli
• Náboj vzniká zelektrizováním tělesa
  • Třením novodurové tyče vzniká záporný náboj
  • Třením skleněné tyče vzniká kladný náboj
  • Uvedená tělesa jsou pouze reprezentativní případy, náboj vzniká i s jinými materiály
• Nabité tělesa na sebe silově působí
  • kladné a kladné resp. záporné a záporné se odpuzují
  • kladné a záporné se přitahují
• Na základě silového působení můžeme i měřit velikost náboje
  • Elektroskop (bez stupnice)
  • Elektrometr (se stupnicí)
  • Přesně měříme měřičem náboje
• Náboj je vždy násobkem elementárního náboje, jenž odpovídá náboji jednoho elektronu
  • $e \approx 1,602 \cdot 10^{-19} C$
• V elektricky neutrálních tělesech jsou celkové počty kladných a záporných elementárních nábojů vyrovnány
  • Jejich účinek se navenek ruší
• Celkový náboj soustavy se při zeelektrování tělesa nemění --> Zákon zachování elektického náboje
• Materiály
  • Izolanty
    • Elektrony jsou pevně vázány na své atomová jádra
  • Vodiče (kovy)
    • Elektrony nejvíce vzdálené od jádra mohou putovat celým tělesem --> dobré vodivé vlastnosti
      • Elektronový plyn

Coulombův zákon

• Popisuje silové působení dvou elektricky nabitých těles

• Používá koncept bodového náboje

  • Možné použít pokud je velikost těles zanedbatelná v porovnání se vzdáleností těles

  

• Z obrázku můžeme vyčíst následující rovnost
  • $F_e = F_G\cdot m\cdot\tan{\alpha}$
• Pokud bychom přemisťovali těleso na tyči tak se $\alpha$ bude měnit.
  • Pozorováním můžeme zjistit, že $F_e$ je nepřímo úměrná poloměru
• Pokud budemě měnit náboje dojdeme k tomu, že $F_e$ je přímo úměrná absolutní hodnotě součinu nábojů
• Tyto pozorování a měření provedl v r. 1784 CH. A. Coulomb a formuloval Coloumbův zákon
  • Velikost elektrických sil kterými na sebe působí dva bodové náboje je přímo úměrná absolutní hodnotě součinu jejich velikostí a nepřímo úměrná druhé mocnině jejich vzdáleností
  • $F_e=k\cdot \frac{ \lvert Q_1 \cdot Q_2 \rvert }{ r^2 }$
  • Konstanta k závisí na prostředí ve kterém se soustava nachází
    • Pro vakuum má hodnotu $k=8,9876 \cdot 10^9 N \cdot m^2\cdot C^{-2} \approx 9\cdot 10^9 N \cdot m^2 \cdot C^{-2}$
    • Někdy je účelné konstantu vyjádřit jako permitivitu vakua
      • $k= \frac{1}{4\pi\epsilon_0}$
      • $\epsilon_0$ si vyjádříme jako $\epsilon_0=\frac{1}{4\pi k} \approx 8,85 \cdot 10^{-12} C^2 \cdot N ^{-1} \cdot m^{-2}$
    • Pro vakuum má tedy Coulombův zákon tvar
      • $F_e= \frac{1}{4\pi\epsilon_0}\cdot \frac{ \lvert Q_1 \cdot Q_2 \rvert }{ r^2 }$
    • Obecný tvar pro izolované látkové prostředí - dielektrikum
      • $F_e= \frac{1}{4\pi\epsilon_r\epsilon_0} \cdot \frac{ \lvert Q_1 \cdot Q_2 \rvert }{ r^2 }$
    • Kde $\epsilon_r$ je relativní permitivita
      • $\epsilon_r$ udává kolikrát se v daném prostředí zeslabí elektrostatické působení
      • Pro vakuum je hodnota $\epsilon_r=1$
      • Pro ostatní prostředí platí $\epsilon_r>1$(Hodnoty uvedené v tabulkách)
      • Přitažlivé síly jsou tedy mimo vakuum menší

Elektrické pole

Intenzita elektrického pole

• Zavádíme za učelem zjištění silového působení na nabitá tělesa v elektrickém poli
• Je určena jako podíl elektrické síly jaká by v daném místě působila na bodový náboj, a tohoto náboje
  • $\vec{E}=\frac{\vec{F_e}}{q}$
  • $[E]=\frac{[F_e]}{[q]}=N\cdot C^{-1}$ jednotkou je tedy $N\cdot C^{-1}$
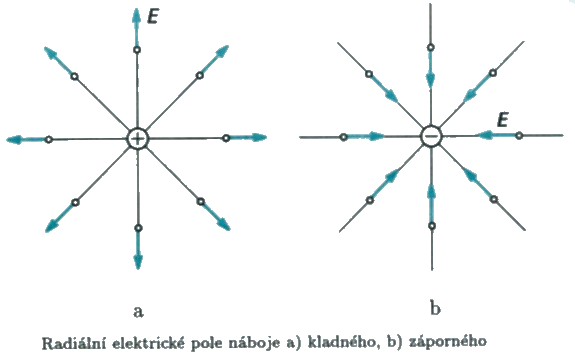
• V případě, že je náboj kladný směřuje vektor $\vec{E}$ steje jným směrem jako $\vec{F_E}$ [obrázek a)] v opačném případě opačně [obrázek b)]
• Velikost intenzity elektrického pole ve vzdálenosti $r$ od osamoceného bodového náboje $Q$ na základě Coulombova zákona
  • $F_e= \frac{1}{4\pi\epsilon_r\epsilon_0}\cdot \frac{\lvert Q \cdot q\rvert}{r^2}$
  • $E=\frac{F_e}{\lvert q\rvert}=\frac {1}{4\pi \epsilon_0 \epsilon_r} \frac{\lvert Q\rvert}{r^2}$
• Směr vektoru $\vec{E}$ závisí na znaménku náboje Q
• Siločáry elektrického pole jsou křivky směřující z místa náboje do nekonečna, či obráceně
  • Siločáry směřují z kladného pólu do záporného, resp. mohohou končit či začínat v nekonečnu
  • Hustotou siločar můžeme měřit intenzitu elektrického pole
• Vektorový model elektrického náboje vypadá následovně
  • jde o pole radiální *
• Elektrické pole můžeme zobrazit například na železných pilinách
  • Elektrony v jednotlivých pilinách se přesunou a vytvoří elektrický dipól
  • Elektrické dipóly se seřadí ve tvaru vektorů intenzity a vytvoří obraz siločár
    • Siločárové modely používáme k zoobrazení elektrického pole
    • Siločáry vystupují z kladně nábitého tělesa a ústí do záporně nabitého
• Radiální elektrické pole
  • 1 bodový náboj
• Homogení elektrické pole
  • 2 stejně nabité desky
  • Intenzita tohoto pole je všude stejně velká a má stejný směr
• 2 shodně nabité náboje
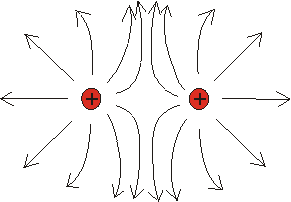
• 2 různě nabité náboje
• Výsledná hodnota intenzity elektrického pole je vektorový součet všech intenzit elektrického pole vůči všem nabitým tělesům

Práce v elektrickém poli

• Práci v homogenním elektrickém poli spočteme jako sílu po dráze
  • Těleso se samo od sebe pohybuje pouze ve směru intenzity elektrického pole
  • Síla je elektrická síla kterou nabité těleso přitahuje jiné nabité těleso ($F_E$)
  • Dráha je vzdálenost dvou nabitých desek ($d$)
    • $W=F_e\cdot d= \lvert q\rvert\cdot E \cdot d$
  • $q$ je náboj tělesa jenž koná práci
  • $E$ je intenzita elektrického pole
• Práce v nehomogením elektrickém poli
  • Dráhu nabytého předmětu si rozdělíme na malé úseky $\Delta s_1$, $\Delta s_2$,...,$\Delta s_n$
  • V těchto úsecích považujeme práci za konstantí
  • V každém úseku sečteme dílčí práci
    • $\Delta W_i=F_i\cdot \Delta s_i \cdot cos\alpha_1=q\cdot E_1 \cdot \Delta s_i \cdot cos\alpha_1$
    • $W_{AB}=\sum\limits_{i=1}^n \Delta W_i$
  • Pokud bychom se vrátili z bodu A do bodu B bude mít práce opačnou hodnotu $W_{BA}=-W_{AB}$
  • Práce nezávisí na trajektorii, po které provádím práci
• Práce je přímo úměrná přenášenému náboji

Elektrické napětí

• Podíl $U_{AB}=\frac {W_{AB}}{q}$ se nazývá elektrické napětí
  • Napětí $U_{AB}$ mezi dvěma body A, B elektrického pole je podíl práce vykonané elektrickou silou při přenesení bodového náboje z bodu A do bodu B a tohoto náboje
  • Možné jen díky tomu, že práce nezávisí na trajektorii
• Jednotka elektrického napětí je volt
  • $[U]=\frac {[W]}{[Q]}=J\cdot C^{-1}=V$
• V homogenním elektrickém poli vykoná elektrická síla při přenesení kladného bodového náboje od kladné k záporné desce práci $W=qEd$ Proto platí následující vztahy mezi $U$, $E$ a $d$
  • $U=\frac{qEd}{q}=Ed$
  • $E=\frac{U}{d}$
• Pro intenzitu elektrického pole můžeme tedy používat jak jednotku $N\cdot C^{-1}$ tak jednotku $V\cdot m^{-1}$

Potenciální energie v elektrickém poli

• Potenciální energi $E_p$ bodového náboje závisí na jeho poloze v elektrickém poli
  • Jde o analagockou věc k potenciální energii v tíhovém poli
    • Změna potenciální energie tak závisí na změně napětí resp. výšky a elektrickém náboji resp. hmotnosti
• Při pohybu ve směru elektrické síly se zmenšuje
• Při pohybu proti směru elektrické síly se zvětšuje
• Jako místo s nulovou $E_p$ volíme zemi, či místa vodivě spojená se zemí
  • $W_{AB}=qU_{AB}=E_{pA}-E_{pB}$
• Napětí mezi body $A$ a $B$ můžeme vyjádřit ve tvaru
  • $U_{AB}=\frac {E_{pA}}{q} - \frac {E_{pB}}{q}$

Elektrický potenciál

• Podíl potenciální energie $E_p$ bodového náboje v určitém místě elektrického pole nazýváme elektrický potenciál $\varphi$ v daném bodě pole
  • $\varphi = \frac{E_p}{q}$
• Napětí mezi dvěma body elektrického pole je rovno rozdílu jejich potenciálů
  • $U_{AB}=\varphi_A-\varphi_B$
  • $[\varphi]=J\cdot C^{-1}=V$
• Potenciál země a uzeměných těles je nulový.
• Podíl práce W, kterou vykonává elektrická síla při přenesení bodového náboje q z daného místa na zem a tohoto náboje
  • $\varphi =\frac{W}{q}$
• Oblasti se stejným elektrickým potenciálem se nazývá Ekvipotenciální plocha
  • V homogením elektrickém poli jsou ekvipotenciální plochy rovnoběžné s rovinou
  • Protože je intenzita elektrického pole stejná mění se potenciál rovnoměrně
  • Zápornou desku můžeme uzemnit
  • Při napětí mezi deskami $U$ a vzdáleností desek $d$ je ve vzdálenosti $x\le d$ od uzeměné desky potenciál
    • $\varphi=U\cdot \frac {x}{d}=E\cdot x$
• V radiálním elektrickém poli
  • jsou ekvipotenciální plochy kulovité se středem v místě náboje
  • V blízkosti náboje je intenzita pole velká a potenciál se mění podél siločáry rychle
  • Ve větší vzdálenosti intenzita pole klesá a potenciál se mění pomaleji
  • Při přiblížení bodového nápoje q k pevnému náboji stejného znaménka Q musíme překonat elektrickou odpudivou sílu (ve vakuu)
  • Soustava spotřebuje práci a zjíská elektrickou potenciální energii
    • $E_p=W=\frac{1}{4\pi \epsilon_0}\frac{Q\cdot q}{r}$
  • Z toho plyne pro potenciál v radiáním poli osamoceném bodového náboje ve vakuu
    • $\varphi=\frac{1}{4\pi \epsilon_0}\frac{Q\cdot q}{r}$

Vodič a izolant v elektrickém poli

Elektromagnetická indukce (vodič v elektrickém poli)

• Pokud vložíme do homogeního elektrického pole dvě dotýkající se kovové destičky na izolačních držadlech
• Při oddělení destiček je měřitelný na každé z nich náboj
• Pokud vložíme do elektrického pole půe vodič, způsobí pole pohyb elektronů ve vodiči -> vznik dočasného eletrického pole
• Tento děj - elektrostatická indukce - trvá tak dlouho dokud je intenzita elektrického pole ve vodiči nulová

Izolant v elektrickém poli

• Izolanty, neboli dielektrika nemají volné elektrony (elektrony se nepřesunují)
• V elektrickém poli se ale posunují jádra atomů ve směru siločar a záprné elektronové obaly proti směru.
• Vznik elektrického dipóly
• Jev se nazývá atomová polarazice dielektrika
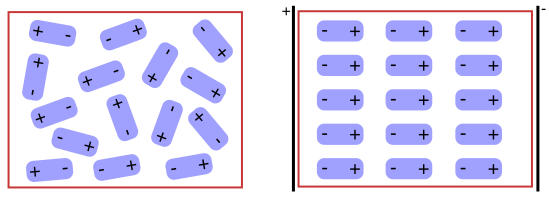
• Molekuly některých látek mají vlastnosti dipólů i mimo elektrické pole
  • Mimo pole jsou neuspořádané
  • V elektrickém poli se uspořádají - orientační polarizace dielektrika
• Polarizace dielektrika způsobuje vznik malé vrstvy záporného náboje u vstupu siločáry a u výstupu siločáry vzniká vrstva nábojů kladných.
  • Tyto náboje jsou vázány na dipóly a nelze je z dielektrika odvést ani oddělit rozdělením dielektrika
• Uvnitř dielektrika náboje promíchány a navenek se neprojevují
• Náboje, jež vznikají v důsledku polarizace na povrchu dielektrika, vytvářejí vnitřní elektrické pole s intenzitou $\vec{E_i}$ namířenou proti intenzitě $\vec{E_e}$ vnějšího pole, jež polarizaci vyvolalo.Výsledná intenzita $\vec{E}$ má směr intenzity $\vec{E_e}$, ale je menší.
  • $\vec{E}=\frac {\vec{E_e}}{\epsilon_r}$ , kde $\epsilon_r$ je relativní permitivita dielektrika
• Elektrické pole se při vložení dielektrika zmenší $\epsilon_r$-krát

Kapacita vodiče

• Při připojení vodiče ke zdroji zjískává vodič stejný potenciál jako zdroj
• Náboj na vodiči je přímo úměrný jeho potenciálu
  • $Q=C\cdot \varphi$
• Veličina $C$ je vlastnost vodiče, jež se nazývá kapacita vodiče
  • $C=\frac{Q}{\varphi}$
• Jednotkou kapacity je farad (F)
  • $[C]=\frac{[Q]}{[\varphi]}=\frac{C}{V}=F$
• Vodič má kapacitu 1 F, jestliže nábojem 1 C nabije na elektrický potenciál 1 V
• Pro vodič o poloměru R ve vakuu platí
  • $\varphi=\frac{1}{4\pi \epsilon_0}\frac{Q}{R}$
  • $\frac{Q}{\varphi}=4\pi \epsilon_0 R$
  • $C=4\pi \epsilon_0 R$
• Kapacita samostatného vodiče je velmi malá

• Proto se používájí kondenzátory *

  Kondenzátor

• Nejjednodušší je deskový kondenzátor bez dielektrika

  • 2 rovnoběžné desky o plošném obsahu $S$ vzdálené $d$ mezi nimiž je vakuum nebo vzduch
• Pokud připojíme deskový kondenzátor ke zdroji nabije se deska s vyšším potenciálem nábojem $+Q$ a deska s menším potenciálem nábojem $-Q$
• Mezi deskami vzniká homogenní elektrické pole o intenzitě
  • $E=\frac{\varphi_1-\varphi_2}{d}=\frac{U}{d}$
• Intenzita pole mezi dvěmi kondenzátory splňuje vztah
  • $E=\frac{\sigma}{\epsilon_0}=\frac{Q}{\epsilon_0 S}$
• Z čehož vyplývá, kde $C_0$ je kapacita kondenzátoru
  • $Q=\frac{\epsilon_0 S}{d}U=C_0U$
• Kapacita deskového kondenzátoru se tedy spočte
  • $C_0=\frac{Q}{U}=\frac{\epsilon_0 S}{d}$
• Při vyplnění prostoru kondenzátoru dielektrikem kapacita kondenzátoru vzrůstá (viz vzorec) $C=\frac{Q}{U}=\frac{\epsilon_0 \epsilon_r S}{d}=\epsilon_r C_0$

• Z tohoto vztahu můžeme zjistit relativní permitivitu dielektrika

  • $\epsilon_r=\frac{C}{C_0}$

  Využití kondenzátorů

• Fotografický blesk
  • Nahromaděná elektrická energie v kondenzátoru se v krátkém časovém okamžiku vybije a způsobí silný světelný záblesk.
• Stabilizační prvek v elektrických obvodech
  • Paralelním zapojením do elektrického obvodu lze dosáhnout vyhlazení napěťových špiček, a tím rovnoměrnějšího průběhu elektrického proudu.
• Odstranění stejnosměrné složky elektrického proudu
  • Větví s kondenzátorem nemůže projít stejnosměrný elektrický proud, ale střídavý proud ano.
• Odrušovací kondenzátor
  • Je nedílnou součástí všech elektrospotřebičů.
  • Používá se samostatně nebo v kombinaci s tlumivkami.
  • Omezuje elektromagnetické rušení vzniklé spínáním nebo rozpojováním elektrického obvodu pod napětím.
• Ladicí součástka v přijímači
  • Změnou kapacity v oscilačním obvodu přijímače se vlastní frekvence obvodu vyrovná vnější frekvenci a dojde k rezonanci, tj. k zesílení přijímaného signálu.
• Počítačová paměť *Paměť složená z velkého množství miniaturních kondenzátorů je schopna uchovat informaci ve formě 0 a 1 (0 = není náboj, 1 = je náboj).
• Defibrilátor
  • Přístroj používaný v lékařství k provádění elektrických šoků při maligních srdečních arytmiích, kdy velké množství náboje projde během krátké doby přes srdeční sval a dojde tak k depolarizaci všech jeho vláken, po níž by se měl obnovit sinusový rytmus.

• Časovače

  • většina generátorů střídavého signálu využívá kondenzátory jako součástky, jejichž střídavé nabíjení a vybíjení určuje periodu kmitů

  Průmyslové kondenzátory

• Rozlišujeme podle druhu dielektryka

  • plastická fólie
  • sklo
  • slída
  • keramika
  • elektrolyt
    • Hliníkové nebo tantalové fólie mezi nimiž je vrstva papíru napuštěná elektrolytem
    • Na jedné fólii vrstva oxidu sloužící jako dielektrikum
    • Na malou tloušťku velká kapacita ($10^{-6} F$ až $10^{-2} F$)
• Otočné
  • Proměná kapacita
  • Otáčením se mění velikost plochy desky

Zapojení kondenzátorů

• Paralelně
  • všechny se nabíjí na napětí zdroje $U$
    • $Q=Q_1+Q_2=UC_1+U C_2=U(C_1+C_2)$
  • Soustava se chová jako jediný kondenzátor s kapacitou $C$
    • $C=C_1+C_2$
• Sériově
  • Součet napětí na kondenzátorech dává celkové napětí
    • $U=U_1+U_2=\frac{Q}{C_1}+\frac{Q}{C_2}=Q(\frac{1}{C_1}+\frac{1}{C_2})=\frac{Q}{C}$
  • Soustava se chová jako jediný kondenzátor s kapacitou $C$
    • $\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}$
    • $C=\frac{C_1C_2}{C_1+C_2}$

Počáteční energie kondenzátorů

• Při připojení nabitého kondenzátoru k žárovce se žárovka rozsvítí
• Kondenzátor se vybíjí, takže napětí je průměrně $\frac{1}{2}U$
• Celková elektrická práce $W$ a také počáteční energie pole kondenzátoru je tedy $E_e$
  • $W=E_e=\frac{1}{2}UQ=\frac{1}{2}\frac{Q^2}{C}=\frac{1}{2}CU^2$