Stacionární magnetické pole

• Magnetické účinky známé už ve starověku (Permanentní magnety, mag. pole země)
• Magnetické pole je pole jehož zdrojem jsou pohybující se elektricky nabité částice
• Podstata objevena v roce 1820 H.CH. Oerstedem
• Oerstedův pokus
  • Oersted umístil drát nad střelku kompasu a a se vychýlila
  • 
• A.M. Ampére zjistil, že na sebe silově působí
  • Vodiče (kterými prochází el. proud) s magnety
  • Vodiče (kterými prochází el. proud) a vodiče (kterými prochází el. proud)
• Procházející proud tedy vytváří v okolí vodiče magnetické pole
  • Pro popis magnetického pole použijeme magnetické indukční čáry
    • Prostorově orientované křivky, jejíž tečna v daném bodě má směr magnetické síly
      • Můžeme je zobrazit na např. železných pilinách
      • 
    • Směřuje od jižního magnetického pólu magnetky (S) k severnímu (N)
    • U vodiče použijeme amperovo pravidlo pravé ruky
      • Palec pravé ruky umístíme ve směru (dohodnutého) toku el.proudu a prsty ukazují směr magnetických indukních čar
      • 
    • Magnetické indukční čáry jsou uzavřené křivky
      • pole vírové

Magnetická indukce

• Magnetické pole podobně jako ostatní pole (elektrické, gravitační) způsobuje působení sil na tělesa.
• Velikost této síly budeme řešit v homogenním magnetickém poli
  • V praxe však pole nejsou homogenní, tak jde pouze o model

Magnetická síla

• Mějme vodič v homogenním magnetickém poli
• Magnetická síla je přímo úměrná délce vodiče
  • Pokud vodič rozdělíme na n části je magnetická síla n-krát menší
• Magnetická síla je přímo úměrná na proudu, který prochází vodičem
• Vzorec pro magnetickou sílu je
  • $F_m=B\cdot I\cdot l$
• Veličina $B$ je magnetická indukce
• Směr síly určíme Flemingovým pravidlem levé ruky
  • Prsty směřují v dohodnutém směru toku proudu
  • ze zhora do dlaně míří vektor magnetické indukce
  • Palec ukazuje směr magnetické síly
• 

Magnetická indukce

• Vektorová veličina kvantitativně popisující magnetické pole
• Vyjadřuje vliv magnetického pole na pohybující se částici s nábojem nebo magnetickým dipólovým momentem
• $B=\frac{F_m}{I\cdot l}$ (pouze pro případ kdy je vodič kolmý s mag. indukčními čárami)
• $[B]=\frac{[F_m]}{[I]\cdot [l]}=\frac{N}{A\cdot m}=T$
• Jednotka je Tesla ($T$)
  • Velká jednotka
  • Země - $10^{-5}T$
    • Přesto velké účinky (Polární záře, odklon kosmické
• K pojmu magnetické indukce jsme došli s předpokladem, že je vodič kolmý na magnetické indukční čáry
  • Pokud je vodič rovnoběžný tak $F_m=0$
• Obecně platí
  • $F_m=B\cdot I\cdot l\cdot \sin \alpha$
  • kde$\alpha \in < 0 ; \pi>$
  • Magnetická síla je kolmá jak na vodič tak na vektor magnetické indukce ($B$) a i na magnetické indukční čáry
  • Tento vztah platí pouze pro přímý vodič s proudem
• Vodič libovolného tvaru
  • Určíme magnetické síly ($\Delta F_m$), které pousobí na velmi krátké úseky ($\Delta F_m$)
  • Výsledná síla je vektorovým součtem všech ($\Delta F_m$)
  • Pro velikost síly platí vztah (Ampérův zákon)
  • $\vert \Delta F_m \vert =B\cdot I\cdot \Delta l\cdot \sin \alpha$
    • kde $\alpha$ je úhel $\vec B$ a směru proud
  • 

Magnetická indukce pole přímého vodiče

• Vektor $\vec B$ velmi dlouhého přímého vodiče leží v rovině kolmé k vodiči a má směr tečny k magnetické indukční čáře
• Velikost $\vec B$ ve vzdálenosti $d$ spočteme
  • $\vert \vec B \vert= \mu \cdot \frac{I}{2 \cdot \pi \cdot d}$
  • $\mu$ je konstanta, která charakterizuje prostředí ve kterém vzniká magnetické pole okolo vodiče
    • Permeabilita prostředí
      • Ve vakuu $\mu_0= 4\cdot \pi \cdot 10^{-7} N \cdot A^{-2}$
    • Pro srovnání různých prostředí používáme relativní permeabilita prostředí ($\mu_r$)
      • $\mu_r=\frac{\mu}{\mu_0}$
    • jde o poměrovou veličinu (nemá jednotku)
      • udává kolikrát je magnetická indukce v látce větší nebo menší než ve magnetická indukce ve vaku

Silové působení dvou vodičů, kterými prochází el. proud

• V magnetickém poli přímého vodiče umístíme další vodič
  • Oba vodiče na sebe působí magnetickou silou
    • souhlasný směr proudu - přitahují se
    • nesouhlasný směr proudu - odpuzují se
    • 
  • $F_m=\frac {\mu}{2\cdot \pi} \cdot \frac {I_1 \cdot I_2}{d} \cdot l$
    • $I_1$ a $I_2$ jsou proudy ve vodičí
    • $d$ je vzdálenost vodičů
    • $l$ je část délky velmi dlouhého vodiče

Ampér

• Jedna ze základních jednotek SI
• Definice:
  • Ampér je stálý elektrický proud, který při průchodu dvěma přímými rovnoběžnými nekonečně dlouhými vodiči zanedbatelného kruhového průřezu umístěnými ve vakuu ve vzájemné vzdálenosti 1 metr vyvolá mezi nimi stálou sílu o velikosti $2 \cdot 10^{-7}$ newtonu na 1 metr délky vodiče

Částice s nábojem v magnetickém poli

• Proud ve vodiči je tvořen nabitými částicemi (elektrony)
  • Magnetická síla je tedy součtem magnetických sil na jednotlivé elektrony
  • Vzorec pro jeden elektron vyjádříme následně
    • Vodič má délku $l$ a je v něm $N$ volných elektronů.
    • Celkový náboj elektronů je $Q=-e\cdot N$
    • Tyto elektrony se ve vodiči pohybují rychlostí $v$ ve směru vodič.
    • Vzdálenost $l$ urazí za dobu $t=l/v$
    • Z toho vyplývá: $I=\frac{\vert Q \vert}{t}=\frac{N\cdot e \cdot v}{l}$
    • To dosadíme do vzorce pro magnetickou sílu
      • $F_m=B\cdot I \cdot l \cdot sin \alpha=B\cdot \frac{ e \cdot v}{l} \cdot l \cdot sin \alpha=B\cdot e\cdot v \cdot sin \alpha$
      • Tento vztah udává mag. sílu, která působí na jeden elektron
      • Tento vztah neplatí pouze pro částice ve vodiči, ale i v prostoru.
        • Pro směr $F_m$ využijeme
          • a) Pro kladně nabitou částici Flemingovo pravidlo levé ruky
          • b) Pro záporně nabitou částici pravou ruku

Pohyb částice v magnetickém poli

• Pokud se částice pohybuje v magnetickém a/nebo elektrickém poli působí na ní Lorentzova síla ($F_L$)
  • $F_L=F_e+F_m=q \left(E + v \times B\right)$
• Využití pohybu částic v magnetickém poli a výskyt v přírodě
  • CRT monitory a televize
  • Urychlovače částic
  • Magnetické pole země odpuzuje nabité částice
    • Kolem pólů pole slabší
      • projev částic v atmosféře - Polární záře
      • Díky magnetickému poli mohl na zemi vzniknout život
        • Oprana před kosmickým zářením

Hallův jev

• Magnetická síla nepůsobí na celý vodič, ale na elektrony
  • Vzniká napětí mezi stranami vodiče
  • 
  • 
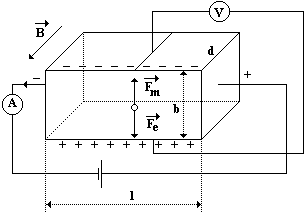
  • Hallovo napětí je při stálém proudu přímo úměrné magnetické indukci
    • $U_H=k\cdot B$
    • $k$ je konstanta závislá na hustotě nosičů náboje
      • U kovů malá
      • U polovodičů významná
        • Využití pro:
          • Teslametry
          • Snímač určující okamžik zapálení směsi ve válci v motoru

Magnetické vlastnosti látek

• Elektrony vytváří elementární magnetické pole
• Součet těchto polí dává dohromady celkové magnetické pole
• Uspořádáním elektronů (typické pro každou látku) se magnetické pole může navzájem i vyrušit
• Látky dělíme podle magnetických vlastností následovně

Diamagnetické látky

• Skládají se z diamagnetických atomů (elementární magnetické síli jsou vyrušeny)
• relativní permeabilita je mírně menší než 1 ($\mu_{r_{Cu}}=0,999990$)
• mírně zeslabují magnetické pole
• některé kovy (měď, zlato, rtuť aj.), nekovové materiály (sklo), kapaliny, plyny, většina organických látek

Paramagnetické látky

• Skládají se z paramagnetických atomů (elementární magnetická pole se ruší jen částečně)
• Jejich relativní permeabilita je mírně větší než 1 ($\mu_{r_{Al}}=1,000023$)
• Atomy paramagnetických látek mají své vlastní magnetické pole
  • Nejdou uspořádat, kvůli tepelnému pohybu
    • Nemohou zesilovat magnetické pole
• Většina kovů (např. sodík, draslík, platina, hliník), některé soli v krystalickém stavu a jejich roztoky, některé plyny (např. vzduch) a další látky

Feromagnetické látky

• mají paramagnetické atomy
  • Uspořádané tak, že značně zesilují magnetické pole
• Relativní permeabilita má velkou hodnotu $(\mu_r \in < 10^2 ; 10^5 > )$
• Některé druhy oceli mají $\mu_r$ 8000 až 15000
• Již slabým polem je možno vytvořit uspořádání atomů, které magnetické pole zesiluje
  • magnetizace látky
    • Příčinou je působení výměnných sil mezi sousedními atomy
    • Atomy se spontánně uspořádávají do magnetických domén $(10^{-3} mm^3$ až $10 mm^3)$
    • Působením magnetického pole se domény orientují souhlasně
    • Objem domén se zvětšuje až do vymizení doménové struktury (látka je magneticky nasycena)
    • 
• Nejdůležitější vlastnosti
  • 1) Feromagnetismus se projevuje jen v krystalickém stavu. Jde o vlastnost struktury látek.
  • 2) Pro každou feromagnetickou látku existuje teplota, nad kterou již se feromagneticky nechová (Curieova teplota)
  • Pro železo je to 770°C
• Fermagnetických látek není mnoho (železo, nikl, kobalt, některé jejich slitiny a některé slitiny jiných kovů)
• Používají se v
  • jádrech cívek v elektromagnetech, transformátorech
  • elektrických strojích
• Ferity (ferimagnetické látky)
  • Sloučeniny oxidu železitého ($Fe_2O_3$) s oxidy jiných kovů
  • $(\mu_r \in < 10^2 ; 10^3 > )$
  • Větší elektrický odpor než ostatní feromagnetické látky
    • Uplatnění v slaboproudé elektrotechnice
      • jádra cívek ve vysokofrekvenčních obvodech
    • A jako permanentní magnety